【３分で理解】ポーカーにおける期待値と計算方法

初心者でも正しく期待値を理解できるように難しい内容は省略しできるだけ簡単に解説します。

期待値とは

期待値とは、1回の試行で得られる値の平均です。

つまり、

期待値がプラスであれば長期的にみて利益がある。

期待値がマイナスであれば長期的にみて不利益である。

と整理できます。

例

ここで例を二つ出してみます。

【１】コインを投げて表が出たら100円もらうことができ、裏が出たら100円を払うゲームがあるとします。期待値はプラスでしょうか？マイナスでしょうか？

ここでの式は、次のとおりです。

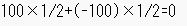
つまり、期待値は「０」となり、このゲームをやっても長期的にみて利益は「０円」なので、やってもやらなくてもいいと判断できます。

【２】サイコロを投げた時に出た目に対して以下のとおりもらえるまたは払うゲームがあります。このゲームは期待値がプラスのゲームでしょうか？

ここでの式は、次のとおりです。

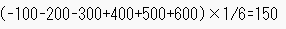
つまり、期待値は「150」となり、このゲームを1回行うことにより、平均すると150円手に入るゲームであることから、長期的にみて利益が出るゲームと言えます。

ポーカーにおける期待値計算

前提として、ポーカーは状況によって期待値計算が複雑になり、期待値（以下、EVと省略）を正しく毎回計算することは難しいです。

そのため、今回は、基本的なポーカーにおける期待値の考え方を理解すれば問題ありません。

例

あなたのスタックは100＄でK♡K♦を持っているとします。

ボードは、2♡2♦2♧　3♡3♦です。

ポットには、既に50＄あります。

リバーで、相手が100＄のオールインをしてきました。
※この時の相手のオールインは、AA,QQ,JJのどれかであるとします。

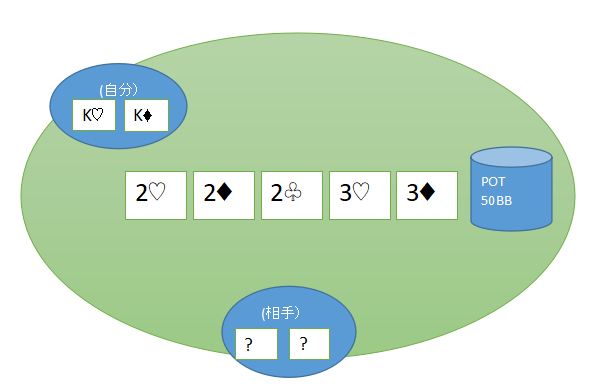
あなたはコールすべきでしょうか？

もちろんあなたは、コールすると答えられると思いますが、今回の目的はEVを正しく理解することですので、なぜ、コールが正解か考えてみましょう。

まずは現状を整理します。

相手に負けているハンド：AA（計６コンボ・・・A♡♦　A♡♧　A♡A♠　A♦A♧　A♦A♠　A♧A♠）
相手に勝っているハンド：QQ,JJ（計12コンボ・・・AAと同様６通りずつあるため）

負けいてる場合は、マイナス100＄、勝った場合は、プラス250＄です。

ここでの式は次のとおりです。

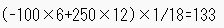
つまり、EVは、133となり、毎回コールすると平均として、133＄プラスであるということがわかります。

以上から、このような時は、コールすべきであるという解になります。

まとめ

今回は、期待値について３分で分かるように、簡潔にまとめました。

ポーカーとは、期待値を理解し、期待値がプラスである選択を取ることが重要になるゲームです。

とは言っても、強い方でも期待値が全て計算して、毎回その通りプレーできているわけではありませんので、まずは期待値を正しく理解することで十分だと思います。

もっと詳しく知りたいという方は、ほかの記事でもポーカー上達方法についてまとめていますので、参考にしてみてください。

それでは。